ARIMA

全称为AutoRegressive Integrated Moving Average Model，即差分整合移动平均自我回归模型。

算法原理

\(\mathtt{ARIMA}\)模型实际上可分为三个部分，\(\mathtt{AR}\)模型就是最经典的回归分析，\(\mathtt{I}\)表示差分，\(\mathtt{MA}\)则使用回归分析的方法来拟合误差。三个部分并非一定要同时使用，应区分不同情况以获得最好的预测效果。

非季节性\(\mathtt{ARIMA}\)模型（Non-seasonal ARIMA models）一般被记为\(\mathtt{ARIMA}(p,d,q)\)，其中\(p\)，\(d\)，\(q\)均非负，分别表示\(\mathtt{AR}\)模型的阶数，差分的阶数以及\(\mathtt{MA}\)模型的阶数。季节性\(\mathtt{ARIMA}\)模型（Seasonal ARIMA models）被记为\(\mathtt{ARIMA}(p,d,q)(P,D,Q)_m\)，其中\(m\)表示每个周期中的观测数量。对于某些具有“季节性”特征的数据，例如周期性的涨落，应用季节性\(\mathtt{ARIMA}\)模型效果可能更好。

\(\mathtt{ARIMA}(p',q)\)的基本形式如下：

\[X_t-\alpha_1X_{t-1}-\cdots-\alpha_{p'}X_{t-p'}=\epsilon_t+\theta_1\epsilon_{t-1}+\cdots+\theta_q\epsilon_{t-q}\]

引入滞后算子\(L\)，可简化为：

\[(1-\sum^{p'}_{i=1}\alpha_iL^i)X_t=(1+\sum_{i=1}^q\theta_iL^i)\epsilon_t\]

其中，\(X_t\)为时间序列，\(\epsilon_i\)为误差项，\(\alpha_i\)为\(\mathtt{AR}\)模型中的参数，\(\theta_i\)为\(\mathtt{MA}\)模型中的参数。

差分

统计学中的差分是一种应用于非平稳时间序列到平稳时间序列的变换，目的是使其在均值意义上更加平稳，即消除非恒定的趋势。\(\mathtt{ARIMA}\)模型中，一般采用一阶或二阶差分，以增强原时间序列的平稳性。对于季节性\(\mathtt{ARIMA}\)，需要采用季节性差分，也即\(X_t-X_{t-T}\)。

\(\mathtt{AR}\)模型与\(\mathtt{MA}\)模型

单独的\(\mathtt{AR}\)模型建立如下：

\[X_t=\alpha_1X_{t-1}+\alpha_2X_{t-2}+\cdots+\alpha_pX_{t-p}+\epsilon_t\]

这里的\(\epsilon_t\)为误差，需要符合白噪声的特征，也即随机扰动。此时当前的值是完全通过历史值来预测的。

单独的\(\mathtt{MA}\)模型建立如下：

\[X_t=\epsilon_t+\theta_1\epsilon_{t-1}+\cdots+\theta_q\epsilon_{t-q}\]

\(\epsilon_t\)为噪声的序列，这里\(X_t\)被表示成一个\(q\)阶的移动平均，与历史值无关系，而只依赖于历史噪声的线性组合。

考虑一个特殊的、无穷阶的\(\mathtt{AR}\)模型：

\[X_t=\epsilon_t+\theta X_{t-1}-\theta^2X_{t-2}+\theta^3X_{t-3}-\theta^4X_{t-4}+\cdots\]

上式中令\(t\leftarrow t-1\)，再与原式相消，得

\[X_t=\epsilon_t+\theta\epsilon_{t-1}\]

即为一个\(\mathtt{MA}(1)\)模型。进一步，可以得出结论：\(\mathtt{MA}(q)\)相当于一个\(\mathtt{AR}(\infty)\)模型。反之也有类似的结论成立。因此，如果拓展\(\mathtt{AR}\)的阶数至无穷阶，那么\(\mathtt{ARMA}\)就会退化为基本的线性回归模型。

算法步骤

1. 平稳性检验

   • ADF（单位根平稳性）检验：检验序列中是否存在单位根，如果存在，那么可以认为就是非平稳时间序列，否则为平稳时间序列。

     这里的单位根指差分方程对应的特征根。

   • KPSS（Kwiatkowski–Phillips–Schmidt–Shin）检验

   通过平稳性检验，可以确定差分的阶数，也即参数\(d\)的值。

2. 确定\(\mathtt{ARMA}\)模型的阶数

   \(p\)和\(q\)的值可通过PACF（partial autocorrelation function，偏自相关）ACF（sample autocorrelation function，自相关）来确定。

   观察PACF序列，如果其在第\(p'\)个值后截尾，那么取\(p=p'\)；观察ACF序列，如果其在第\(q'\)个值后截尾，那么取\(q=q'\)。

   截尾指序列从某个时间点开始，突然变得非常小。

   拖尾指序列以指数率单调递减或震荡衰减。

   对于不太好观察或判断截尾或拖尾的情形，可以通过AIC（Akaike information criterion (AIC)）和/或BIC（Bayesian Information Criterion）来判断\(p,q\)的取值。

   \[\left\{ \begin{align} \mathtt{AIC} &= n\log(\frac{\mathtt{SSE}}{n})+2(p+q+k)\\ \mathtt{BIC} &= n\log(\frac{\mathtt{SSE}}{n})+(p+q+k)\log(n) \end{align} \right.\]

   其中，\(\mathtt{SSE}\)表示均方误差和，\(n\)表示样本总数，\(p+q+k\)表示模型的参数总数，当存在常数项时\(k=1\)，否则\(k=0\)。

   \(\mathtt{AIC}\)和\(\mathtt{BIC}\)用来检验模型的效果，同时针对参数的数量加上一个惩罚项。对于不同的模型（选用不同的\(p,q\)），\(\mathtt{AIC}\)以及\(\mathtt{BIC}\)较小的模型更优。

3. 模型构建与预测：选用之前确定的参数\(p,d,q\)构建\(\mathtt{ARIMA}\)模型，预测数据及其置信区间。

实例

考虑对一段时间序列的预测。

首先需要选择合适的\(d\)值。

% use adftst and kpsstest to find appropriate value for d
function rd = findD(data, dmax)
    rd = -1;
    for d = 0:dmax
        adfOut = adftest(data);
        kpssOut = kpsstest(data);
        if (adfOut == 1 && kpssOut == 0)
            rd = d;
            break;
        end
        data = diff(data);
    end
end

再通过\(\mathtt{AIC}\)和\(\mathtt{BIC}\)选择出\(p,q\)的值。

% use AIC and BIC to find appropriate value for p and q
% p in [0, pmax], q in [0, qmax]
function [rp, rq] = findPQ(data, pmax, qmax, d)
    data = reshape(data, length(data),1);
    LOGL = zeros(pmax+1, qmax+1);
    PQ = zeros(pmax+1, qmax+1);
    for p=0:pmax
        for q=0:qmax
            try
                model = arima(p,d,q);
                [~, ~, logL] = estimate(model, data);
                LOGL(p+1,q+1) = logL;
                PQ(p+1,q+1) = p+q;
            catch
                LOGL(p+1,q+1) = inf;
                PQ(p+1,q+1) = 0;
            end
        end
    end
    LOGL = reshape(LOGL, (pmax+1)*(qmax+1),1);
    PQ = reshape(PQ, (pmax+1)*(qmax+1),1);
    [aic, bic] = aicbic(LOGL, PQ+1, length(data));
    aic = reshape(aic, (pmax+1), (qmax+1));
    bic = reshape(bic, (pmax+1), (qmax+1));

    aicmin = min(aic(:));
    [aicx, aicy] = find(aic==aicmin);
    aicx = aicx(1); aicy = aicy(1);
    bicmin = min(bic(:));
    [bicx, bicy] = find(bic==bicmin);
    bicx = bicx(1); bicy = bicy(1);
    if (aicx^2+aicy^2 < bicx^2+bicy^2)
        rp = aicx; rq = aicy;
    else
        rp = bicx; rq = bicy;
    end
end

最后，建立\(\mathtt{ARIMA}\)模型进行预测。

function res = myarima(data, m)
    d = findD(data, 3);
    if (d == -1)
        disp("Unable to find valid d");
        exit();
    end
    [p, q] = findPQ(data, 4, 4, d);
    disp([p d q])
    model = arima(p, d, q);
    estModel = estimate(model, data');
    [forcastData, YMSE] = forecast(estModel, m, data');
    res = forcastData;
end

对同一段时间序列（长为20），分别采用\(\mathtt{ARIMA}\)与灰色预测，结果如下。可以看到，对最初的一段序列，\(\mathtt{ARIMA}\)与灰色预测的结果相当吻合，后续的趋势也始终保持一致。

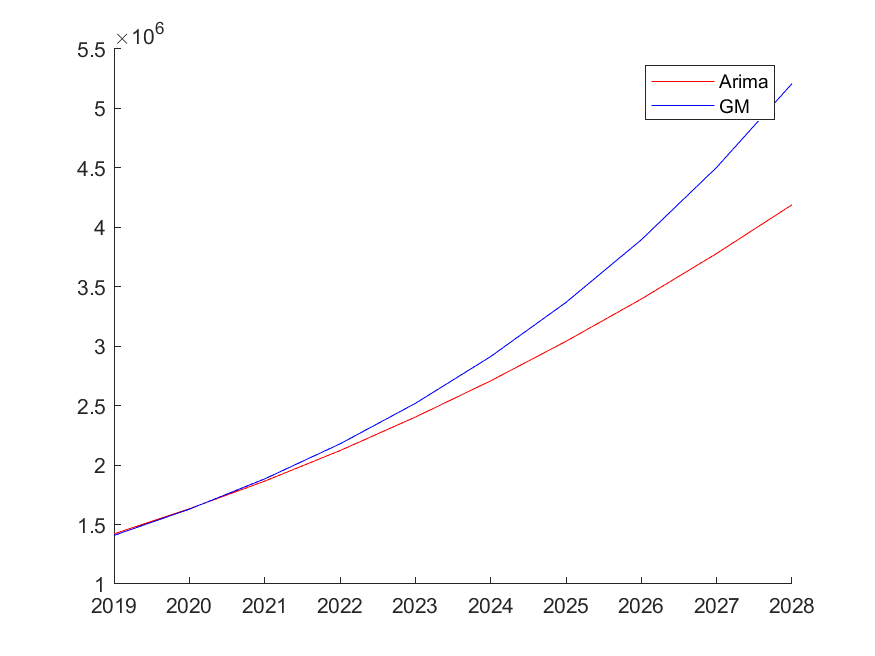
适用范围

一般来说，序列预测相关的问题都可以采用\(\mathtt{ARIMA}\)进行求解。时间序列越平稳，\(\mathtt{ARIMA}\)模型的预测效果越好。

另外，在实际预测时，除了时间序列外，还可以引入其他的可能会对模型产生影响的参数，这样的被拓展的模型称为\(\mathtt{ST-ARIMA}\)，即时空\(\mathtt{ARIMA}\)。