2019 Problem D
Problem:Time to leave the Louvre
题目背景
ICM团队正在帮助设计法国巴黎卢浮宫的疏散计划。一般来说,疏散的目标是让所有人员尽快安全地离开建筑物。
卢浮宫是世界上最大、参观人数最多的艺术博物馆之一,2017年接待了超过810万游客。卢浮宫有五层,其中两层在地下,包括一个主要出入口以及供会员使用的三个出入口。
疏散计划面临几个重要的挑战:
- 博物馆的参观人数一年四季都在变化。
- 游客具有多样性——说多种语言、团体旅行、残疾游客等。
- 只有应急人员和博物馆工作人员知道可用出口点的总数(包括员工出入口、紧急出入口、秘密出入口等)。公众对这些出入口的认识增加可以帮助疏散,但是同时也会引起安全问题,因为相较于四个主要的出入口,这些出入口的安保水平较低。
提供的数据
提供了一个网站Affluences,网站上会实时更新每个入口的预计等待时间(但是目前该网站已经下线了)。
问题
-
开发一个紧急疏散模型,使博物馆能够探索疏散游客的一系列选择,同时允许紧急救援人员尽快进入建筑物。模型需要具有较强的适应性,可以用于解决各种类型的潜在威胁。
较为合适的应该是仿真模拟型的模型,例如细胞自动机。
-
确定向出口移动的潜在瓶颈。
-
验证模型,讨论卢浮宫将如何实施它。提出卢浮宫应急管理的政策,包括合适的人群管理和控制方法等。此外,讨论如何将模型调整应用到其他类似的大型建筑物中。
Paper #1900007
论文框架与思路
-
Introduction
- 问题重述,提出了三个目标:
- 找到最优的疏散方案
- 确定潜在的瓶颈
- 使模型一般化
- 文献综述,简单叙述了一些有关于室内疏散的现有模型
- Our work,总结论文中提出的模型与结果
- 问题重述,提出了三个目标:
-
Preparation of the models
提出假设,主要是在对问题进行必要的化简。
- 简化卢浮宫的结构。将每一层简化为一个U形的结构,并且场地中所有位置均是可以通行的(不考虑场地中摆放的艺术品等障碍),同时假设其中所有的楼梯与电梯等在功能和结构上完全一致。
- 简化人群的结构。假设人群随机分布,在同一时刻逃生并且完全听从指挥。假设只存在三类人群,分别为老人、年轻人、残疾人。
-
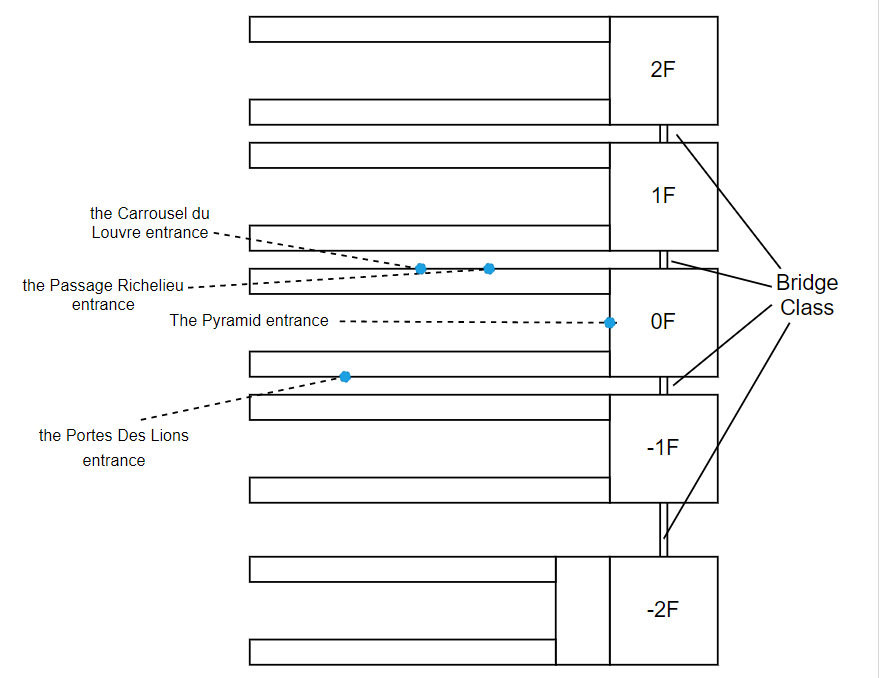
The 2D Island-Bridge Model
-
Dimensionality Reduction,“降维”
将每个楼层视为一个“岛”,楼层之间的通道视为“桥”。进一步简化问题,假设两个“岛”之间存在一对“连接点”(junction point),连接着两个“岛”的“桥”就横跨在这两个点之间。根据这一连接点到初始时各个通道的距离,“桥”的等效长度可视为各通道长度的一个加权平均:
\[\eta_i=\frac{dis(i,junc)}{\sum_{i=1}^ndis(i,junc)}\\ (Length)_{eq}=\frac{1}{n}\cdot\sum_{i=1}^n[\eta_i\cdot(length)_i]\\ (Width)_{eq}=\frac{1}{n}\sum_{i=1}^n(width)_i\] -
Spacial Discretization,空间离散化
a中得到了简化后的平面图,共有五个区域分别代表五个楼层,相邻楼层之间有通道连接。将整个区域离散化成一个个结点(类似于网格化),人员只能从某个结点移动到与其相邻的另一个结点。
-
Dijkstra算法,求到出口的最短路径
Dijsktra是图论中经典的单源最短路算法,时间复杂度为\(O(n\log n)\)。
论文中对Dijsktra算法做了部分修改(实际上是修改了图和出口的参数,并没有修改算法本身)。首先是增加了一个Visual Range的概念,也即将所有长度大于Visual Range的边设置为不可达,以及所有处于危险区中的边也设置为不可达(疏散时,可能存在某个危险区,例如火源所在区域)。此外,给出口加上了一个限制\(\alpha\in(0,1)\),表示最多只能有比例为\(\alpha\)的人员从该出口逃生。
通过以上方法,可以求出对于任何一个点,其应该被疏散的出口以及路径。对于不同类型的人员,其存在不同的逃生速度,加权平均后可以求出个人平均疏散时间:
\[\bar{t}=\frac{\mathtt{sum}(dis)}{\mathtt{sum}(people)\cdot\sum_k(P_k\cdot v_k)}\]其中,\(\mathtt{sum}(dis)\)表示所有人的疏散路径长度之和,\(\mathtt{sum}(people)\)表示总人数,\(P_k、v_k\)分别表示不同人群所占的比例以及逃生速度。
-
Danger Index Model
将离散化后的点进一步简化为mesh,也即一小片包含多个点的区域,考虑如何计算这一区域的危险指数。分为三个部分:
\[\left\{ \begin{align} w_{\mathtt{density}}^{(i)}&=\frac{N_{\mathtt{mesh}}^{(i)}}{\pi\times R_{\mathtt{mesh}}^2}\\ w_{\mathtt{emergeny}}^{(i)}&=\frac{1}{dis(i,E_{xy})}\\ w_{\mathtt{exit}}^{(i)}&=\min \{dis(i,Exit^{(s)})\} \end{align} \right.\\ \mathtt{DI}^{(i)}=a\cdot w_{\mathtt{density}}^{(i)}+b\cdot w_{\mathtt{danger}}^{(i)} + c\cdot w_{\mathtt{exit}}^{(i)}\]其中,\(w_{\mathtt{density}}^{(i)}\)用来衡量人群密度,\(w_{\mathtt{emergeny}}^{(i)}\)是到危险点的距离的倒数,\(w_{\mathtt{exit}}^{(i)}\)是到最近的出口的距离。最后的危险指数\(\mathtt{DI}\)是三者的线性组合。论文中指出,刚开始疏散时,危险点的影响很大,因此\(b\)的取值也应相应大一些;后续危险点的影响下降,可以相应地下调\(b\)。
-
How to Utilize Additional Exits?
给危险指数设定一个阈值,计算所有超过阈值的区域中的总人数\(P_{\mathtt{danger}}\),给\(P_{\mathtt{danger}}\)设置一系列区间,当落在不同的区间时,开放不同数量的额外出口。
论文中没有提到额外出口对于危险指数的影响,也没有试图取研究额外出口的位置,或是区间的值应该怎样具体选择。
其实这样是明智的,如果考虑的话,模型会变得非常复杂,这与此前不停简化的思想就相悖了。
-
How to Let Emergency Personnel Enter?
这一部分没有提出新的算法或是改进模型,只是简单指出急救人员应当如何进入。论文中主要提出两点:急救人员应当从占用率低的出入口以及那些未开放的出入口进入;进入后,急救人员应当从危险指数低的区域向危险指数高的区域移动,实时的危险指数可以通过Danger Index Model计算出。
-
Model Evaluation and Sensitivity Analysis
研究了模型的三个参数人员密度\(\rho_{people}\)、危险区范围\(R_{dead}\),出口的最大使用比例\(\alpha\)对不同人群平均逃生时间的影响。
实验结果说明,人员密度和危险区范围大小对逃生时间几乎没有影响。
但是这可能是因为模型有一个地方不太合理:模型在判断出口是否拥塞时,采用的是通过的人员的比例,而非绝对数量,因此不管人员密度多大,通过各个出口的比例不会变,自然对逃生时间就不会有影响。
论文中也确实做了一个实验,发现当人员密度增大时,出入口1(主出入口)的通过人数显著上升。虽然这没有超过模型中对逃生人数比例的限制,但是在实际中显然是不合适的。
-
-
The 3D Cellular Automata Model
论文中提出,做这一部分的目的是,2D-IBM model过于抽象,所以需要3D model来“intuitively simulate the evacuation process”,并且3D可视化后得到的一些结果,可以间接用来证明此前的某些假设的合理性。首先使用AutoCAD来画了一个卢浮宫的3D图,再用Pathfinder(一个软件,专门用来模拟人员移动)来模拟人员的疏散,这一软件的原理就是细胞自动机。
实验结果,发现了瓶颈一般位于楼梯以及出入口的附近,并且基于人员密度画出的热点图与此前的危险指数结果相似,间接证明危险指数的设置是比较合理的(大概意思是人员聚集得比较多的地方更危险)。
-
Strengths and Weaknesses
-
Strengths,主要谈了模型简化的合理性、模型的鲁棒性(例如,模型考虑了不同人群的特点,并且对于人员密度、危险区大小不敏感)、3D可视化的效果。
-
Weaknesses,Dijkstra算法需要对每个点都做,耗时较长;对空间点离散化方法合理性的讨论(离散成一个个点后,人员的移动反映在实际空间其实是在跳跃“leap”)。
其实解决空间点离散化的合理性,简单地把点取得更密就可以了,似乎也没有别的方法,当然这样算法的耗时也会增加。
-
-
Conclusion
提出对疏散政策的建议。
- 增加传感器的数量,使得可以实时检测馆内各个场所的人员密度变化等情况,以确保策略的有效性。
- 在“Affluences” app中增加一个引导功能,根据所在位置实时规划游客的疏散路线。
- 保证所有的出入口、楼梯应当处于良好状态,不会因为被堵塞而不可用(针对模型发现的出入口和楼梯容易成为瓶颈的结论)。
优点与缺点
-
论文中提出的模型实际上是非常简单的,但是整篇文章结构非常清晰,所用的语言也很准确、地道(但是少数地方有些重复,比如把模型的结构重复叙述了好几遍),感觉写作水平很高。
不停的简化问题就是本文的思路(当然简化需要是合理的),虽然最后的模型本质上非常简单,但是能够把原先非常复杂的场景抽象成简单的问题,并且思路还非常清晰,值得学习。
-
论文中的很多模型应该是自己设计的,比如危险指数的判定,其实这些应该可以体现出论文的创新性。只要合理并且结果还不错,我们也不是一定都要采用现成的模型,至少也应该根据问题的实际情况调整一下。
-
如果论文中只有2D的模型,似乎已经足够了,但是3D的可视化做出来确实让研究结果增色不少。
- Dijkstra那里算法设置似乎不太合理,有些地方有误。比如Dijskstra是单源最短路算法,可以同时求出某个点到四个出口的最短路径。visual range论文中给出的值是21m,结合实际情况似乎这个值有点小(?),但是如果变大,我怀疑按照Dijkstra算法的原理,visual range就起不到作用了。判定拥堵的算法似乎也有小问题,论文中说的是针对每个点分别做Dijkstra,但是后文说不同的人群移动速度不同,因此并非距离出口越近的点就一定越先到达出口(并使得出口发生拥塞)。为了考虑速度的问题,其实在2D的时候就可以引入细胞自动机来模拟疏散了。
- 题目中游客的多样性还提到了“说多种语言”等,这些也应当加入模型中,并且应对的策略应该也不复杂(例如简单地在出口的指示牌上加上多种语言?)。