元胞自动机（Cellular Automata，CA）

算法原理

元胞自动机采用离散的空间布局和离散的时间间隔，将元胞分成有限种状态，元胞个体状态的演化，仅与其当前状态以及其某个局部领域的状态有关。元胞自动机研究的是大量并行单元个体组成的复杂系统的宏观行为与规律。

特点：平行计算、局部性、一致性

包含的基本要素： $A=(L,d,S,N,f)$ $L$为元胞空间，$d$为元胞自动机内元胞空间的维数，$S$是元胞有限的、离散的状态集合，$N$为某个领域内所有元胞的集合，$f$为局部映射或局部规则，也即每个元胞与周围元胞间的相互作用。

根据状态的演化，元胞自动机分为平稳型、周期型、混沌型和复杂型。

算法步骤

定义元胞的初始状态。
定义系统内元胞的变化规则$f$。
设置仿真时间，输出仿真结果。

实例

生命游戏，Conway’s Game of Life，1970，康威

细胞有两种状态，存活或者死亡。若当前细胞为存活状态，则当其周围存活细胞低于两个或超过三个时（模拟生命数量过多或过少），该细胞变成死亡状态；若当前细胞为死亡状态，当其周围有三个存活细胞时，该细胞变成存活状态（模拟繁殖）。

clc, clf, clear
  
plotbutton = uicontrol('Style','pushbutton', ...
    'String','Run', ...
    'FontSize', 12, ...
    'Position', [100, 400, 50, 20], ...
    'Callback', 'run=1;');
  
erasebutton = uicontrol('Style','pushbutton', ...
    'String', 'Stop', ...
    'FontSize', 12, ...
    'Position', [180, 400, 50, 20], ...
    'Callback', 'freeze=1;');
  
quitbutton = uicontrol('Style','pushbutton', ...
    'String', 'Quit', ...
    'FontSize', 12, ...
    'Position', [260, 400, 50, 20], ...
    'Callback', 'stop=1; close;');
  
resetbutton = uicontrol('Style','pushbutton', ...
    'String', 'Reset', ...
    'FontSize', 12, ...
    'Position', [340, 400, 50, 20], ...
    'Callback', 'reset=1;');
  
number = uicontrol("Style",'Text', ...
    'String', '1', ...
    'FontSize', 12, ...
    'Position', [20, 400, 50, 20]);
  
n = 128;
z = zeros(n, n);
sum = z;
cells = (rand(n, n) < .2);
imh = image(cat(3, cells, z, z));
axis equal
axis tight
  
x = 2:n-1;
y = 2:n-1;
stop = 0;
run = 0;
freeze = 0;
reset = 0;
while (stop == 0)
    if (run == 1)
        sum(x, y) = cells(x, y-1) + cells(x, y+1) + ...
            cells(x-1, y) + cells(x+1,y) + ...
            cells(x-1, y-1) + cells(x-1,y+1) + ...
            cells(3:n, y-1) + cells(x+1,y+1);
        cells = (sum == 3) | (sum == 2 & cells);
        set(imh, 'cdata', cat(3, cells, z, z))
        stepnumber = 1 + str2num(get(number, 'string'));
        set(number, 'string', num2str(stepnumber));
    end
    if (freeze == 1)
        run = 0;
        freeze = 0;
    end
    if (reset == 1)
        run = 0;
        reset = 0;
        cells = (rand(n, n) < .2);
        set(imh, 'cdata', cat(3, cells, z, z));
        set(number, 'string', num2str(1));
    end
    drawnow
end

兰顿蚂蚁，Langton’s ant，兰顿，2000

由黑白格子和一只蚂蚁构成。蚂蚁随机位于其中一格中。若蚂蚁位于白格，则其将该格改为黑色，右转90度并向前一格；若蚂蚁位于黑格，则将该格改为白色，左转90度并向前一步。实验证明，蚂蚁留下的路线会出现许多对称或重复的形状。

while (stop == 0)
    randx = mod(randx, n);
    randy = mod(randy, n);
    if randx == 0
        randx = n;
    end
    if randy == 0
        randy = n;
    end
    if (run == 1)
        if (cells(randx, randy) == 0)
            direction = direction + 1;
            if (direction > 4)
                direction = 1;
            end
        else
            direction = direction - 1;
            if (direction < 1)
                direction = 4;
            end
        end
        cells(randx, randy) = 1 - cells(randx, randy);
        randx = randx + dx(direction);
        randy = randy + dy(direction);
        set(imh, 'cdata', cat(3, cells, z, z))
        stepnumber = 1 + str2num(get(number, 'string'));
        set(number, 'string', num2str(stepnumber));
    end
    if (freeze == 1)
        run = 0;
        freeze = 0;
    end
    if (reset == 1)
        run = 0;
        reset = 0;
        cells = z;
        randx = ceil(rand() * n);
        randy = ceil(rand() * n);
        direction = ceil(rand() * 4);
        set(imh, 'cdata', cat(3, cells, z, z));
        set(number, 'string', num2str(1));
    end
    drawnow
end

教室逃生

给定一间教室，一个出口，教室中有若干障碍物，数量为$m$的学生需要从出口逃生，要求同一时刻任两个学生不能处于同一位置。

while (stop == 0)
    while (escaped < m)
        if (run == 1)
            [xs, ys, vals] = sortXYVal(xs, ys, vals); % student near the exit should be operated first
            for i=1:m
                if (status(i) == 1)
                    continue
                end
                students(xs(i), ys(i)) = 0;
                [nextx, nexty, nextStatus] = findNextStep(xs(i), ys(i), val, students, n);
                xs(i) = nextx;
                ys(i) = nexty;
                status(i) = nextStatus;
                if (status(i) == 0)
                    students(xs(i), ys(i)) = 1;
                else
                    escaped = escaped + 1;
                end
            end
            set(imh, 'cdata', cat(3, 1 - students, 1 - cells, 1 - cells))
            stepnumber = 1 + str2num(get(number, 'string'));
            set(number, 'string', num2str(stepnumber));
        end
        if (freeze == 1)
            run = 0;
            freeze = 0;
        end
        if (reset == 1)
            run = 0;
            reset = 0;
            students = cells;
            status = zeros(m);
            escaped = 0;
            [xs, ys, vals] = initStudent(m, n, val);
            for i=1:length(xs)
                students(xs(i), ys(i)) = 1;
            end
            set(imh, 'cdata', cat(3, 1 - students, 1 - cells, 1 - cells))
            set(number, 'string', num2str(1));
        end
        drawnow
    end
    disp(['escaped rounds' num2str(stepnumber)])
    run = 0;
    escaped = 0;
end

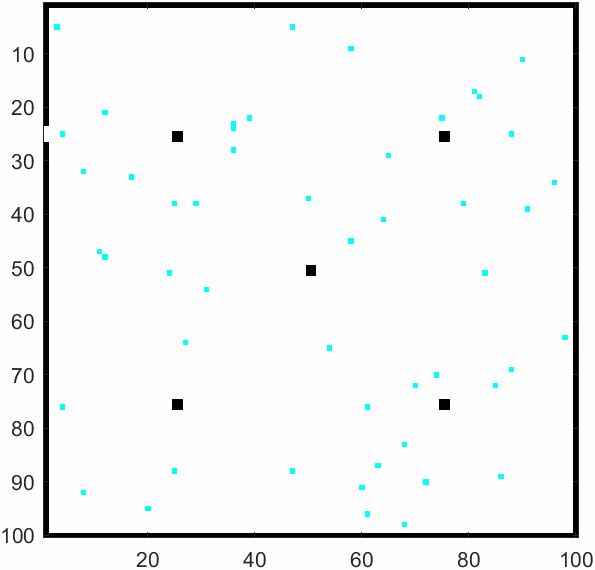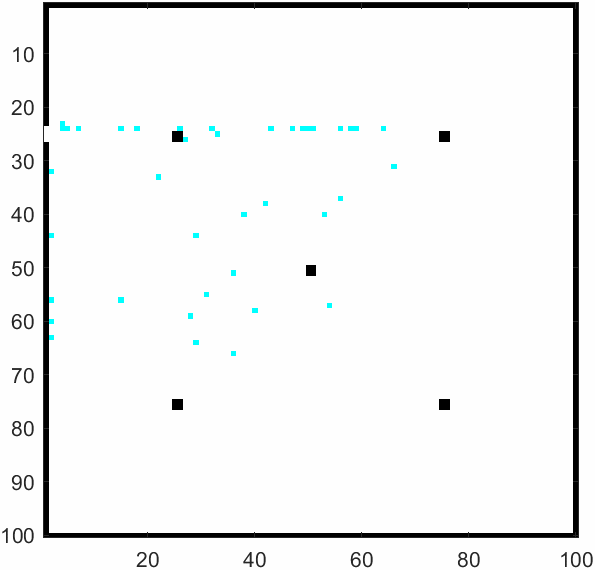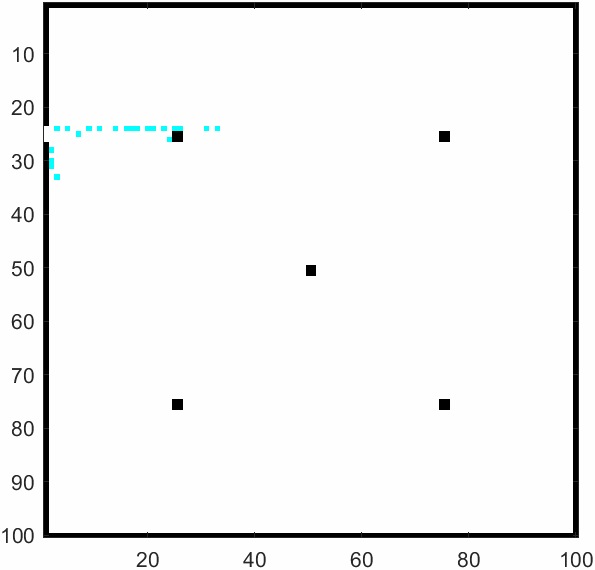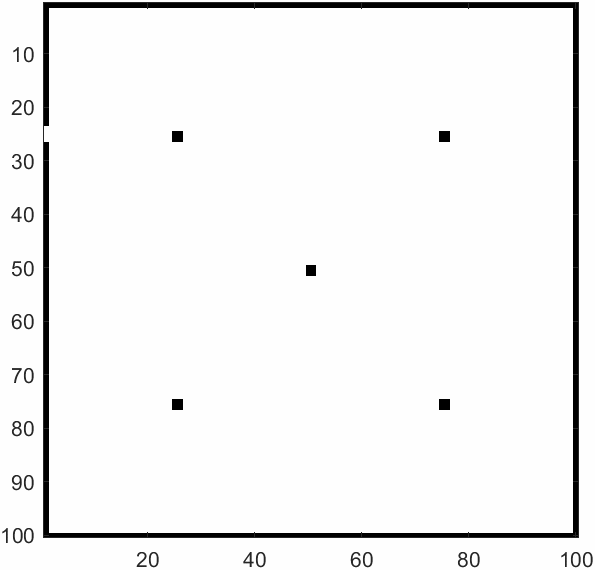
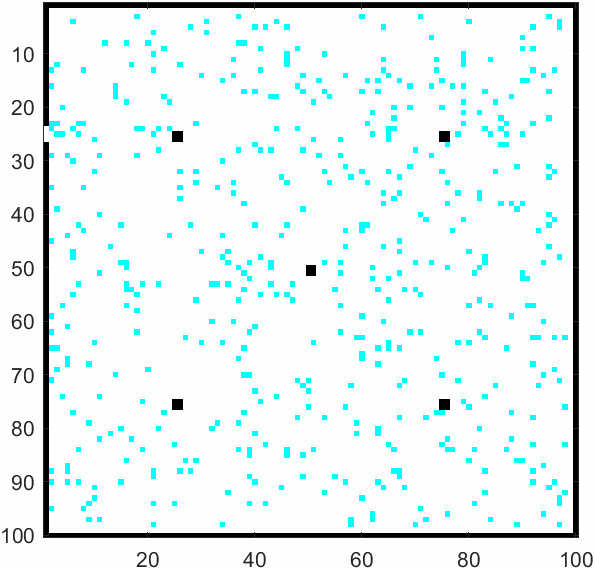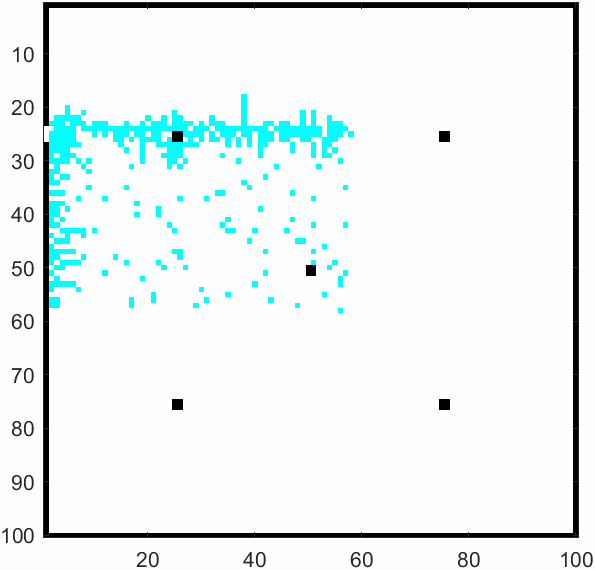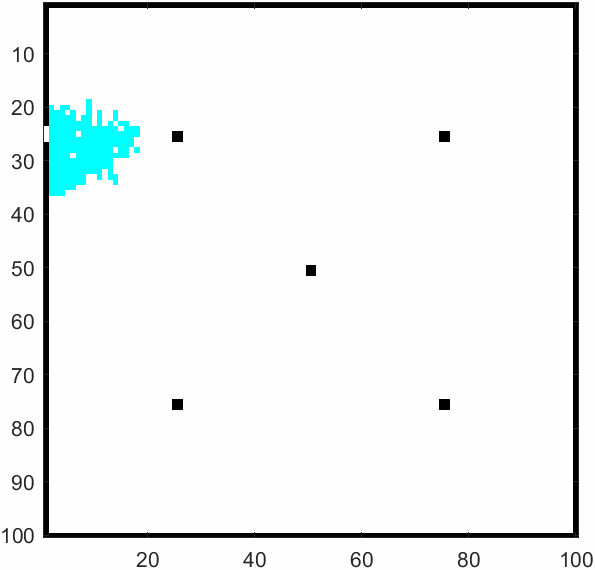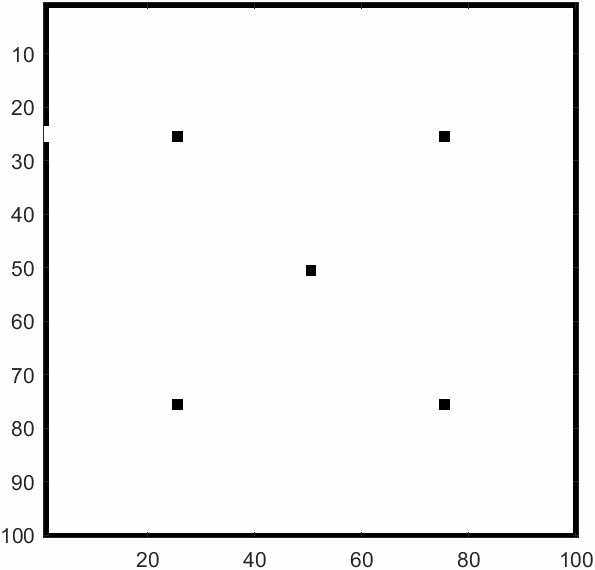
$m=50$及$m=500$时的模拟结果如上。元胞自动机可以模拟出每个学生的逃生过程，以及全部逃生需要花费多少时间。

适用范围

细胞自动机属于仿真型机理建模，当遇到一个非典型的数学建模问题，例如沙漠变迁、逃生、病毒传播、模拟火灾等，尤其是开放度比较高的问题，通常就需要考虑机理仿真了。

此前的所有算法，例如遗传、模拟退火等都属于分析型的算法，与这种仿真建模适用范围有所不同。