灰色预测(Gray Model,GM)
算法原理
灰色模型,介于完全信息透明的“白色模型”与完全信息闭塞的“黑色模型”之间。通过少量的、不完全的信息,建立灰色模型,以对其做出长期的预测,便是灰色预测。
灰色预测包括时间序列预测、灾变预测等。灰色模型的记号为\(G(M,N)\),其中\(N\)表示变量的个数,\(M\)表示常微分方程的阶数。时间序列预测的灰色模型即为\(G(1,1)\),也是最为常见的灰色模型。
灰色关联系数
考虑数列\(x_j=(x_j(1),x_j(2),\cdots,x_j(n))\),及\(x_i=(x_i(1),x_i(2),\cdots,x_i(n))\),定义二者的关联系数:
\[\xi_{ij}(k)=\frac{\min_{j}\min_k|x_j(k)-x_i(k)|+\rho\max_{j}\max_k|x_j(k)-x_i(k)|)}{|x_j(k)-x_i(k)|+\rho\max_j\max_k|x_j(k)-x_i(k)|}\]\(|x_j(k)-x_i(k)|\)被称为海明距离。\(\rho\)通常在\([0,1]\)内取值。定义相关度为: \(r_{ij}=\frac{\sum_{k=1}^{n}\xi_{ij}(k)}{n}\)
其中,\(r_{ij}\)大于0称为正相关;\(r_{ij}\)小于0称为负相关。\(|r_{ij}|>0.7\)称为强相关,\(|r_{ij}|<0.3\)称为弱相关。进一步可以得到相关度矩阵: \(R=\begin{pmatrix} r_{11} & r_{22} & \cdots & r_{1n}\\ r_{21} & r_{22} & \cdots & r_{2n}\\ \vdots & \vdots & & \vdots\\ r_{n1} & r_{n2} & \cdots & r_{nn} \end{pmatrix}\)。
算法步骤
设原始序列为\(x^{0}=(x^{(0)}(1),x^{(0)}(2),\cdots,x^{(0)}(n))\)。
-
累加得新数列
\[x^{(1)}(k)=\sum_{i=1}^kx^{(0)}(i),k=1,2,\cdots,n\] -
求灰导数方程
\[\mathbf{d}(k)=\frac{x^{(1)}(k) - x^{(1)}(k-1)}{k-(k-1)}=x^{(0)}(k)\]由此可见,在预测时,如果下一项\(x^{(1)}(k+1)\)与\(x^{(1)}(k)\)之间发生了跳跃,误差就会比较大。因此,灰色模型\(G(1,1)\)只适用于连续、平滑的事件趋势中。如果出现突变或者灾变,就需要用到灾变灰色模型。
-
定义紧邻均值\(z^{(1)}\)
\[z^{(1)}(k)=\frac{x^{(1)}(k)+x^{(1)}(k-1)}{2},k=2,3,\cdots,n\] -
定义灰微分方程
\[\mathbf{d}(k)+az^{(1)}(k)=b\]也即
\[x^{(0)}(k)+az^{(1)}(k)=b\quad(*)\]依次代入\(k=2,3,\cdots,n\),令\(\mathbf{Y}=\begin{bmatrix}x^{(0)}(2) & x^{(0)}(3)&\cdots&x^{(0)}(n)\end{bmatrix}^T\),\(\mathbf{u}=(a,b)^T\),\(\mathbf{B}=\begin{bmatrix}-z^{(1)}(2)&1\\-z^{(1)}(3)&1\\\vdots&\vdots\\-z^{(1)}(n)&1\end{bmatrix}\),则有\(\mathbf{Y}=\mathbf{Bu}\)。由最小二乘法可求解出\(a,b\):
\[\widetilde{\mathbf{u}}=(\widetilde{a},\widetilde{b})^T=(\mathbf{B}^T\mathbf{B})^{-1}\mathbf{B}^T\mathbf{Y}\] -
白化\(GM(1,1)\)模型
白化,指将\(x^{(0)}(k)\)不再看成是离散的数列,而是关于\(k\)连续的函数,这样\(x^{(1)}(k)=\int_1^kx^{(0)}(t)dt\),从而有\(\mathbf{d}(k)=\frac{dx^{(1)}}{dk}=x^{(0)}(k)\)。再用\(x^{(1)}(k)\)代替\(z^{(1)}(k)\),\((*)\)式化为:
\[\frac{dx^{(1)}}{dk}+ax^{(1)}=b\]将求出的\(a,b\)代入上式中,即可得到灰色模型。需要注意的是,由于我们的模型不是经过严密的数学推导出来的,因此使用时需要非常谨慎,只有符合一阶线性常微分方程的数列或者矩阵才能用灰色模型来预测。
-
求解模型
变形得
\[\frac{dx^{(1)}}{dk}=-a(x^{(1)}-\frac{b}{a})\]令\(X=x^{(1)}-\frac{b}{a}\),及初值条件\(k=0,x^{(1)}=x^{(1)}(1)=x^{(0)}(1)\),可得
\[x^{(1)}(k)=[x^{(0)}(1)-\frac{b}{a}]e^{-ak}+\frac{a}{b}\]再等间隔取样以离散化,得
\[\widetilde{x}^{(1)}(k+1)=x^{(1)}(k)=[x^{(0)}(1)-\frac{b}{a}]e^{-ak}+\frac{a}{b}\quad (**)\]注意这里,\(\widetilde{x}^{(1)}\)的第一项实际上对应\(x^{(1)}\)的第零项。
累减还原得原始数据的预测值
\[\widetilde{x}^{(0)}(k+1)=\widetilde{x}^{(1)}(k+1)-\widetilde{x}^{(1)}(k)\] -
模型检验
如5中所述,模型建立之后不能立即使用,而应该先用相关检验的方法去检测模型稳健性及准确性是否达到标准。
-
相对残差\(Q\)检验
定义残差序列\(\epsilon^{(0)}(i)=x^{(0)}(i)-\widetilde{x}^{(0)}(i)\),相对误差序列\(\Delta_i=\frac{\epsilon^{(0)}(i)}{x^{(0)}(i)}\),进而有相对残差
\[Q=\frac{1}{n}\sum_{k=1}^n\Delta_k\]\(Q\)越小,表示模型越精确。
-
方差比\(C\)检验
\[\left\{ \begin{align} S_1^2&=\frac{1}{n}\sum_{k=1}^n[x^{(0)}(k)-\bar{x}]\\ S_2^2&=\frac{1}{n}\sum_{k=1}^n[\epsilon^{(0)}(k)-\bar{\epsilon}] \end{align} \right.\]定义方差比\(C=\frac{S^2_2}{S_1^2}\),\(C\)越小表示模型越精确。
-
小误差概率\(P\)检验
置信水平取0.5,置信区间半长为0.6745,令\(P=P\{|\epsilon-\bar{\epsilon}|<0.6745S_1\}\)。 \(P\)值越大,代表模型的预测越精确。
精度检验对照表如下,一般要求模型的精度等级要达到2级及以上。
等级 相对残差 方差比 小误差概率 1级 <0.01 <0.35 >0.95 2级 <0.05 <0.50 >0.80 3级 <0.10 <0.65 >0.70 -
-
模型的预测
实际应用中,直接代入公式\((**)\)进行计算即可。
\[\widetilde{x}^{(0)}=[\underbrace{\widetilde{x}^{(0)}(0),\widetilde{x}^{(0)}(1),\cdots,\widetilde{x}^{(0)}(n)}_{原数列的模拟},\underbrace{\widetilde{x}^{(0)}(n+1),\cdots,\widetilde{x}^{(0)}(n+m)}_{对未来数列的预测}]\]通过比较对原数列的模拟以及真实的值,我们可以大致得到灰色预测方法的准确度。此外,我们也可以通过计算数列的级比来预先大致判定是否可以用\(GM(1,1)\)来预测:
\[\lambda(k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,3,\cdots,n\]如果大部分\(\lambda(k)\in(e^{-\frac{2}{n+1}},e^{\frac{2}{n+1}})\)内,则说明使用\(GM(1,1)\)来预测可能会有比较好的结果。
实例
给出一段时间序列(10年内的利润),要求预测未来几年的利润。
clear
syms a b; % symbolic scalar variables
c = [a b]';
A = [89677, 99215, 109655. 120333. 135823, 159878, 182321, 209407, 246619, 300670]; % initial sequence
B = cumsum(A);
n = length(A);
m = 10; % predict for the next m items
for i=1:(n-1)
C(i) = (B(i) + B(i+1)) / 2;
end
D = A;
D(1) = [];
D = D';
E = [-C; ones(1,n-1)];
c = (E*E')\(E*D); % use least square to calculate a,b
c = c';
a = c(1); b = c(2);
F = []; F(1) = A(1); % initial condition
for i=2:(n+m)
F(i) = (A(1) - b/a)/exp(a*(i-1)) + b/a;
end
G = []; G(1) = A(1);
for i=2:(n+m)
G(i) = F(i) - F(i-1); % G is the prediction for A
end
最终预测的效果如下:
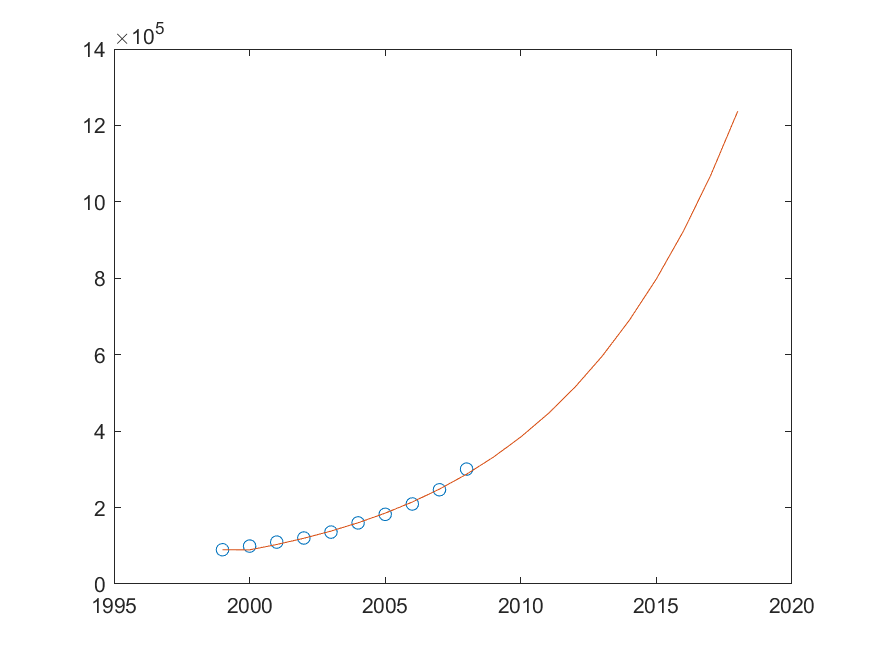
可以看到,对原序列的模拟(前十个点)是相当吻合的,从而此时使用灰色预测的效果较好。
适用范围
\(GM(1,1)\)是对时间序列的预测,适合于连续、平滑的时间序列。对于其他,可通过模型检验以及最终效果来判断是否适用灰色预测模型。