回归，Regression

1.一元回归

1.1线性回归

• 最小二乘法

  Lxx = sum((x-mean(x)).^2);
  Lxy = sum((x-mean(x)).*(y-mean(y)));
  b1 = Lxy/Lxx;
  b0 = mean(y) - b1*mean(x);
  y = b1 * x + b0;
  

• 采用LinearModel.fit

  m2 = LinearModel.fit(x, y);
  y = m2.Coefficients.Estimate(2, 1) * x + m2.Coefficients.Estimate(1, 1);
  

• 采用regress

  Y = y';
  X = [ones(size(x,2),1),x'];
  [b, bint, r, rint, s] = regress(Y, X);
  y = b(2,1) * x + b(1, 1);
  

  r表示残差，bint、rint分别表示系数和残差的置信区间。

1.2一元非线性回归

• 对数形式非线性回归

  m1 = @(b, x) b(1) + b(2) * log(x);
  % beta0 = [0.01;0.01] is the initial estimation for b(1),b(2)
  nonlinfit1 = fitnlm(x, y, m1, [0.01;0.01]);
  b = nonlinfit1.Coefficients.Estimate;
  Y1 = b(1, 1) + b(2, 1) * log(x);
  

• 指数形式非线性回归

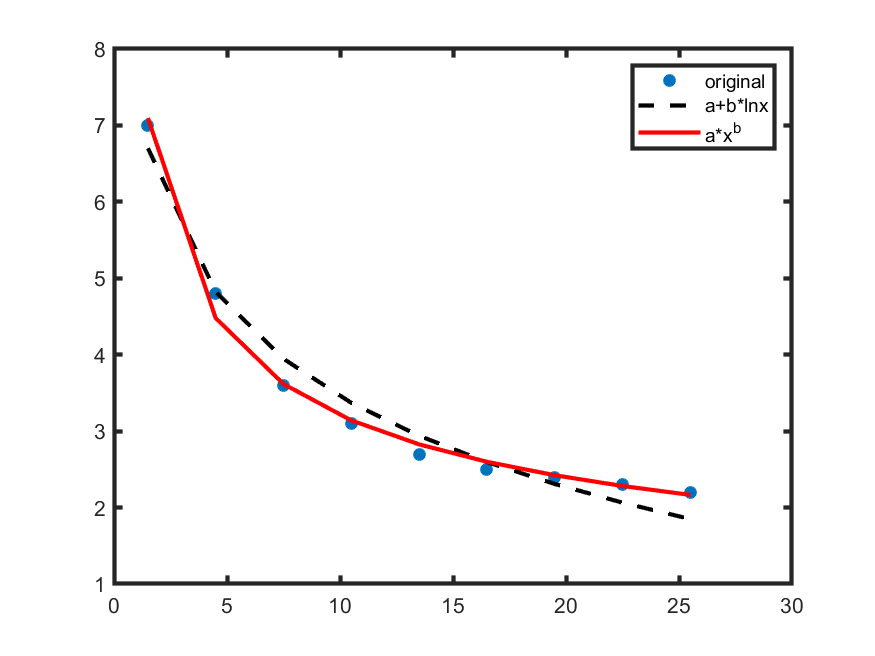
  m2 = 'y~b1 * x^b2';
  nonlinfit2 = fitnlm(x, y, m2, [1;1]);
  b1 = nonlinfit2.Coefficients.Estimate(1,1);
  b2 = nonlinfit2.Coefficients.Estimate(2,1);
  Y2 = b1 * x.^b2;
  

  分别使用对数和指数进行一元非线性回归的一个比较如下：

2.多元回归

直接应用regress()拟合多元回归模型即可。

Y = Y';
X = [ones(n,1), x1', x2', x3'];
[b, bint, r, rint, s] = regress(Y, X, 0.05); % alpha=0.05表示显著性水平

3.逐步回归（Stepwise Regression）

逐步回归是一种可以自动选取变量的拟合方法。通过一些预先指定的标准，例如模型的F检验，来判断某些变量是否应该加入模型中或是从模型中去除。

通常有三种方法：

1. 依次引入变量，判断引入后通过F检验判断模型是否发生显著性变化，如果是，则保留该变量。
2. 与1相反，依次删除变量。
3. 逐步筛选，在1的基础上，如果决定保留变量，再对所有已保留的变量进行T检验，如果该已保留的变量并不因新加入的变量而发生显著性变化，则剔除此变量。

stepwise(X, Y, [], 0.05, 0.10)
% 0.05 及 0.10 是用于显著性检验的参数

4.逻辑斯蒂回归（Logistic Regression）

逻辑函数

\[h_{\theta}(x)=\frac{1}{1+e^{-\theta^Tx}}\]

决策边界即为\(\theta^Tx=0\)。

GM = fitglm(X0, Y0, 'Distribution', 'binomial');
Y1 = predict(GM, X1);

binomial表示二分类。