统计机器学习，Statistical Machine Learning

• 统计机器学习，Statistical Machine Learning
  • 0.什么是统计机器学习
  • 1.\(K\)-近邻分类，KNN
  • 2.朴素贝叶斯方法，NB
  • 3.支持向量机，SVM
    • 3.1.线性可分支持向量机
    • 3.2.线性支持向量机
    • 3.3.非线性支持向量机
    • 3.4.SVM用于求解多类问题
  • 4.决策树，DT
    • 4.1.特征选择
    • 4.2.决策树的生成
    • 4.3.决策树的剪枝
    • 4.4.随机森林

0.什么是统计机器学习

• 输入\(x\in X\)，输出\(y\in Y\)，未知的目标函数\(f:X\rightarrow Y\)
• 训练集\(T=\{(x_1,y_1),\cdots,(x_n,y_n)\}\)
• 假设空间\(H={h_k}\)，学习到的目标函数\(g\in H\)，学习算法\(A\)
• 学习算法\(A\)根据训练集\(D\)从假设空间\(H\)中选择一个最好的\(g\approx f\)

1.\(K\)-近邻分类，KNN

\(K\)-近邻（K-Nearest Neighbors）算法是一种基于实例的分类方法。该算法计算未知样本与每个训练样本之间的距离，取最近的\(K\)个训练样本，用其中出现频率最大的类别作为该未知样本的类别。

\(\mathtt{KNN}\)算法对\(k\)值的依赖较高，其在决策时只与少量的相邻样本有关，因此采用这种方法可以较好地避免样本的不平衡问题。此外，对于类域交叉或重叠较多的待分样本集（例如考虑无法用一个超平面将不同的类分开的情形），就比较合适使用\(\mathtt{KNN}\)进行分类。

matlab实现

knn = ClassificationKNN.fit(Xtrain, Ytrain, 'Distance', 'seuclidean', 'NumNeighbors', 5);
[Y_knn, Yscore_knn] = knn.predict(Xtest);

2.朴素贝叶斯方法，NB

朴素贝叶斯（Naïve Bayes）是一种基于贝叶斯定理进行分类的算法。贝叶斯定理是对先验概率、后验概率之间关系的描述：

\[P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)} \tag{1}\]

设\(x=\{x_1,x_2,\cdots,x_n\}\in X\)，类别集合\(C=(c_1,c_2,\cdots,c_k)\)，朴素贝叶斯方法描述如下：

1. 计算\(P(c_k\)|\(x),k=1,2,\cdots,K\)。
2. 令\(y=\max_k(P(c_k\)|\(x))\)。 也即，最终选取的分类为使得条件概率最大的类别。

由贝叶斯定理，有

\[P(c_k|x)=\frac{P(x|c_k)P(c_k)}{P(x)}=\frac{P(x_1|c_k)\cdots P(x_n|c_k)P(c_k)}{P(x)} \tag{2}\]

其中\(P(x_i\)|\(c_k)\)为先验概率，可以在训练集上计算得到。从上式中也可以注意到，贝叶斯定理要求各个属性之间独立。

朴素贝叶斯方法简单，且在许多场合上分类准确率高，速度快。

matlab实现

dist = repmat({'normal'}, 1, width(A)-1);
dist(catPred) = {'mvmn'};
% mvmn: multivariate, multinomial distribution
Nb = fitcnb(Xtrain, Ytrain, 'Distribution', dist);
Y_Nb = Nb.predict(Xtest);

3.支持向量机，SVM

支持向量机（Support Vector Machine）是一个二类线性分类器，通过间隔最大化来实现分类，而使用核技巧可以实现非线性分类。

3.1.线性可分支持向量机

3.1.1.基本原理

• 分类超平面：\(w^*\cdot x+b^*=0\)

• 决策函数：\(f(x)=\mathtt{sign}(w^*\cdot x + b^*)\)

• 函数间隔：

  设训练集\(T\)和超平面\((w,b)\)，定义超平面关于样本点\((x_i,y_i)\)的函数间隔为：

  \[\hat{\gamma_i}=y_i(w\cdot x_i+b)\]

  定义关于\(T\)的函数间隔为：

  \[\hat{y}=\min_i\hat{\gamma_i}\]

• 几何间隔：\(\gamma_i=\frac{\hat{\gamma_i}}{\|w\|}\)，\(\gamma=\frac{\hat{\gamma}}{\|w\|}\)，其中\(\|w\|\)表示\(w\)的\(L_2\)范数。

• 间隔最大化：

  \[\max_{w,b}\frac{\hat{\gamma}}{||w||}\quad\quad s.t.\quad y_i(w\cdot x_i+b)\geq \hat{\gamma},\quad i=1,2,\cdots,N \tag{3}\]

  而由于函数间隔是可以缩放的，因此不妨设\(\hat{\gamma}=1\)，可将原最大化问题转化如下：

  \[\min_{w,b}\frac{1}{2}||w||^2\quad\quad s.t.\quad y_i(w\cdot x_i+b)\geq1,\quad i=1,2,\cdots,N \tag{4}\]

  是上等式等号成立的点，便称为支持向量。等式成立时有两种情况，分别如下：

  1. \[w\cdot x_i+b=1\]
  2. \[w\cdot x_i+b=-1\]

  二者到分类超平面的几何距离均为\(\frac{1}{\|w\|}\)。

3.1.2.对偶算法

定义拉格朗日函数如下：

\[L(w,b,\alpha)=\frac{1}{2}||w||^2+\sum_{i=1}^N\alpha_i[1-y_i(w\cdot x_i+b)] \tag{5}\]

其中\(\alpha_i\geq0\)，\(\alpha=(\alpha_1,\alpha_2,\cdots,\alpha_N)^T\)为拉格朗日乘子向量。

注意到，当满足\((4)\)中的约束条件时，有

\[\max_{\alpha}(L(w,b,\alpha))= \left\{ \begin{align} &\frac{1}{2}||w||^2,\quad&\forall i,1-y_i(w\cdot x_i+b)\leq0\\ &\infty,&\mathit{other} \end{align} \right. \tag{6}\]

因此，\(\min_{w,b}\max_\alpha(L(w,b,\alpha))\)与\((4)\)等价。

考虑\(\min_{w,b}\max_\mathbf{\alpha}(L(w,b,\mathbf{\alpha}))\)的对偶问题\(\max_{\alpha}\min_{w,b}(L(w,b,\alpha))\)。首先，因为有

\[\min_{w,b}(L(w,b,\alpha))\leq L(w,b,\alpha)\leq\max_{\alpha}(L(w,b,\alpha))\tag{7}\]

进而有

\[\max_{\alpha}\min_{w,b}(L(w,b,\alpha))\leq\min_{w,b}\max_{\alpha}(L(w,b,\alpha)) \tag{8}\]

当满足\(\mathtt{KKT}\)条件时，\((8)\)中的等号成立。\(\mathtt{KKT}\)条件如下：

\[\left\{ \begin{align} &\nabla_{w,b}L(w,b,\alpha)=\mathbf{0}\\ &\alpha_i[1-y_i(w\cdot x_i+b)]=0\\ &[1-y_i(w\cdot x_i+b)]\leq 0\\ &\alpha_i\geq 0\\ &i=1,2,\cdots,N \end{align} \right. \tag{9}\]

因此假设\(\mathtt{KKT}\)条件成立，原问题可转化为对对偶问题的求解。首先对\(w,b\)求偏导，令其为\(0\)得：

\[\begin{align} &\nabla_wL(w,b,\alpha)=0\\ \Rightarrow&w^*-\sum_{i=1}^N\alpha_iy_ix_i=0\\ \Rightarrow&w^*=\sum_{i=1}^N\alpha_iy_ix_i \end{align} \tag{10}\]

又由\(\mathtt{KKT}\)条件，有\(\alpha_i[1-y_i(w\cdot x_i+b)]=0,i=1,2,\cdots,N\)，选择一个\(j,s.t.\alpha_j\neq0\)，代入得：

\[b^*=y_j-w^*\cdot x_j=y_j-\sum_{i=1}^N\alpha_iy_i(x_i\cdot x_j)\tag{11}\]

代入\(w^*,b^*\)，再将目标函数由求极大变换成求极小，问题转化为如下：

\[\begin{align} \min_{\alpha}\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i\\ s.t.\sum_{i=1}^N\alpha_iy_i=0,\alpha_i\geq0,i=1,2,\cdots,N \end{align} \tag{12}\]

这是一个凸二次规划问题，具有全局最优解，可以通过序列最小最优化算法\(\mathtt{SMO}\)进行求解。

求出\(\mathbf{\alpha}\)后，可以得到分离超平面和分类决策函数的表达式如下：

\[\begin{align} &\sum_{i=1}^N\alpha_iy_i(x\cdot x_i)+b^*=0\\ &f(x)=\mathtt{sign}(\sum_{i=1}^N\alpha_iy_i(x\cdot x_i)+b^*) \end{align} \tag{13}\]

注意到，分类决策函数的输出只依赖于输入\(x\)和训练样本输入的内积。根据\(\mathtt{KKT}\)条件，对应\(\alpha_i>0\)的实例\(x_i\)就是支持向量（落在决策边界上）。

3.2.线性支持向量机

在线性可分支持向量机中，要求所有点均满足函数间隔大于等于\(1\)的条件。但对于某些线性不可分的点，可以引入松弛变量\(\xi_i\)，使得：

\[y_i(w\cdot x_i+b)\geq1-\xi_i,\quad \xi_i\geq0,\quad i=1,2,\cdots,N, \tag{14}\]

为了使\(\xi_i\)尽可能小，可以优化目标函数，增加惩罚项，变换为如下，这称为软间隔最大化：

\[\min_{w,b,\mathbf{\xi}}(\frac{1}{2}||w||^2+C\sum_{i=1}^N\xi_i) \tag{15}\]

其中\(C>0\)为惩罚参数。同理，可得到线性支持向量机的对偶问题：

\[\begin{align} \min_{\alpha}\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i\\ s.t.\sum_{i=1}^N\alpha_iy_i=0,0\leq\alpha_i\leq C,i=1,2,\cdots,N \end{align} \tag{16}\]

最后，\(\alpha_i>0\)所对应的样本\(x_i\)称为支持向量。若\(0<\alpha_i<C\)，则\(\xi_i=0\)，\(x_i\)在间隔边界上。若\(\alpha_i=C\)，\(0<\xi_i<1\)，则分类正确，\(x_i\)在间隔边界与分离超平面之间；若\(\alpha_i=C,\xi_i=1\)，则\(x_i\)在分离超平面上；若\(\alpha_i=C,\xi_i>1\)，则\(x_i\)位于误分一侧。

3.3.非线性支持向量机

使用一个变换（核函数），将原空间数据映射到新空间。在新空间使用线性分类方法从训练数据中学习分类模型。非线性支持向量机的对偶问题如下：

\[\begin{align} \min_{\alpha}\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(\mathbf{\phi(x_i)\cdot \phi(x_j)})-\sum_{i=1}^N\alpha_i\\ s.t.\sum_{i=1}^N\alpha_iy_i=0,0\leq\alpha_i\leq C,i=1,2,\cdots,N \end{align} \tag{17}\]

其中\(\phi(x)\)是映射函数，其对应于输入空间\(X\)到特征空间\(H\)的一个映射，使得对所有\(x,z\in X\)，存在核函数\(K(x,z)\)，满足\(K(x,z)=\phi(x)\cdot\phi(z)\)。对于同一个核函数，可能存在多个映射函数与之对应。决策函数如下：

\[f(x)=\mathtt{sign}(\sum_{i=1}^N\alpha_iy_iK(x_i,x)+b^*)\tag{18}\]

常用的核函数包括

• 多项式核函数：\(K(x,z)=(x\cdot z+1)^p\)
• 高斯核函数：\(K(x,z)=\exp(-\frac{\|x-z\|^2}{2\sigma^2})\)

3.4.SVM用于求解多类问题

• 一对多：某类为正例，其余类为负例，构建\(N\)个\(\mathtt{SVM}\)（\(N\)为总类数），分类时将样本分类为具有最大分类函数值的类别。
• 一对一：对任意两类构造一个\(\mathtt{SVM}\)，分类时采用投票法决定类别。
• 层次法：所有类先分成两类，每类再分为两类，以此类推。

matlab实现

svmStruct = fitcsvm(Xtrain, Ytrain, 'KernelFunction','linear', 'KKTTolerance', 0.2);
Y_svm = svmStruct.predict(Xtest);

4.决策树，DT

决策树（Decision Tree）是一种对实例进行分类的树形结构，由节点和有向边组成。节点包括两种，分别为内部节点以及叶节点，前者表示一个特征或是属性，后者表示一个类别。

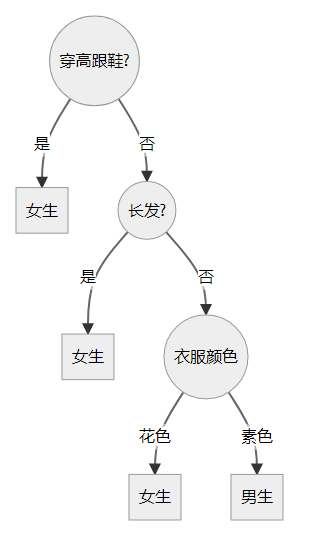
决策树的一个示例

决策树学习实际上就是从训练集中归纳出一组分类规则，得到一个与训练集矛盾较小的决策树。决策树的学习包括特征选择、决策树生成以及决策树剪枝三个过程。

4.1.特征选择

特征选择考虑的是如何选取出分类能力强的特征，分类能力通过信息增益来衡量，也就是某一特征对数据集进行分类时不确定性减少的程度。

随机变量\(X\)的熵定义为：

\[H(X)=-\sum_{i=1}^np_i\log p_i,\quad p_i=P(X=x_i) \tag{19}\]

一般地，熵越低表示\(X\)的不确定性度越低。条件熵如下，表示已知\(X\)时，\(Y\)的不确定性。

\[H(Y|X)=\sum_{i=1}^np_iH(Y|X=x_i) \tag{20}\]

设训练集\(D\)，共有\(K\)个类别\(C_k\)，特征\(A\)有\(n\)个不同的取值\(\{a_1,\cdots,a_n\}\)。根据\(A\)的不同取值将\(D\)划分为\(n\)个子集\(D_1,\cdots,D_n\)，设\(D_{ik}\)表示\(D_{i}\)中属于类\(C_k\)的样本的集合，|\(X\)|表示集合\(X\)的基数。特征\(A\)对数据集\(D\)的信息增益\(g(D,A)\)就定义为：

\[\begin{align} &g(D,A)=H(D)-H(D|A)\\ &H(D)=-\sum_{k=1}^K\frac{|C_k|}{|D|}\log_2\frac{|C_k|}{|D|}\\ &H(D|A)=\sum_{i=1}^n\frac{|D_i|}{|D|}H(D_i)=-\sum_{i=1}^n\frac{|D_i|}{|D|}\sum_{k=1}^K\frac{|D_{ik}|}{|D_i|}\log_2\frac{|D_{ik}|}{|D_i|} \end{align} \tag{21}\]

4.2.决策树的生成

• ID3算法：设有训练集\(D\)，特征集\(A\)，阈值\(\epsilon>0\)

  1. 若\(D\)中所有实例属于同一类\(C_k\)，则\(T\)为单节点树，将\(C_k\)作为该节点的类标记，返回\(T\)。
  2. 若\(A\)为空，则\(T\)为单节点树，将\(D\)中实例数最大的类\(C_k\)作为该节点的类标记，返回\(T\)。
  3. 否则计算\(A\)中各特征对\(D\)的信息增益，选择信息增益最大的特征\(A_g\)。
  4. 如果\(A_g\)的信息增益小于阈值\(\epsilon\)，则置\(T\)为单节点树，将D中实例数最大的类\(C_k\)作为该节点的类标记，返回\(T\)。
  5. 否则对\(A_g\)的每一可能取值\(a_i\)，依\(A_g=a_i\)将\(D\)分割为若干子集\(D_i\)，作为\(D\)的子节点。
  6. 对于\(D\)的每个子节点\(D_i\)，如果\(D_i\)为空，则将\(D\)中实例最大的类作为标记，构建子节点。
  7. 否则令\(D\leftarrow D_i\)，\(A\leftarrow A-{A_g}\)，重新执行1~6步，得到子树\(T_i\)。

  ID3算法存在的问题：信息增益倾向于选择分枝比较多的属性。

• C4.5算法：采用信息增益比来选择特征

  \[\begin{align} &g_R(D,A)=\frac{g(D,A)}{H_A(D)}\\ &H_A(D)=-\sum_{k=1}^n\frac{|D_k|}{|D|}\log_2\frac{|D_k|}{|D|} \end{align} \tag{22}\]

  对于分枝数较多的特征，其对应的\(H_A(D)\)也会较大，从而除以\(H_A(D)\)可以避免偏爱分枝多的属性。

  同时，C4.5增加了对连续值属性的处理。对于连续值属性\(A\)，可找到一个属性值\(a\)，将不大于\(a\)的划分到左子树，大于\(a\)的划分到右子树。

  但是信息增益比也存在问题：其倾向于选择分割不均匀的特征。对此，我们可以先选择\(n\)个信息增益大的特征，再从这\(n\)个特征中选择信息增益比最大的特征。

4.3.决策树的剪枝

为了防止决策树在训练集上过拟合，需要对生成的决策树进行简化，也即（后）剪枝。也就是从已生成的树上裁掉一些子树或者叶节点，将其父结点作为新的叶节点，用其实例数最大的类别作为标记。

设树\(T\)的叶节点个数为|\(T\)|，对树\(T\)的叶节点\(t\)，其有\(N_t\)个样本，其中有\(N_{tk}\)个样本属于类别\(k\)。定义\(H_t(T)\)为叶节点\(t\)上的经验熵：

\[H_t(T)=-\sum_{k=1}^K\frac{N_{tk}}{N_t}\log\frac{N_{tk}}{N_t} \tag{23}\]

定义损失函数

\[C_\alpha(T)=\sum_{t=1}^{|T|}N_tH_t(T)+\alpha|T|=C(T)+\alpha|T| \tag{24}\]

其中，\(C(T)\)表示模型对训练数据的预测误差，|\(T\)|表示模型的复杂程度，\(\alpha\geq0\)为参数，用来在二者之间进行平衡。

决策树的剪枝，也就是选择在验证集上损失函数最小的模型，算法流程如下：

1. 计算每个节点的经验熵。
2. 递归地从树的叶节点向上回缩，如果回缩后的损失函数小于等于回缩前，则剪枝，将父结点变为新的叶节点。
3. 反复进行2，直至不能继续为止，得到损失函数最小的子树\(T_\alpha\)。

4.4.随机森林

由于决策树容易过拟合，因此可采用随机森林，也即由多个决策树组成的分类器，最后通过投票机制来确定分类。

对随机森林中的每棵决策树，假设数据集\(D\)中共有\(N\)个样本，那么对数据集\(D\)进行\(N\)次有放回抽样，就得到训练集\(D'\)。\(D\)中该决策树没有用到的数据便可以作为验证集。